数学组 李震
摘要:数形结合的思想是每年高考考查的重要数学思想之一,它常用来研究方程根的情况,讨论函数的值域(最值)及求变量的取值范围等。运用数形结合思想去解决特定的选择题和填空题特别有效。从近几年的高考题来看,数形结合的重点是研究“以形助数、以数辅形”。 本文从数形结合思想出发,结合具体的数学解题案例进行分析,探讨了数形结合思想在高中数学解题中的应用,旨在为高中数学解题提供参考。
关键词:数形结合思想;高中数学;解题
一、引言
数形结合思想可以解决一些复杂的数学问题,如函数、几何问题等,对于高中数学解题来说具有很重要的意义。数形结合思想可以将复杂的问题简单化,可以提高解题的效率,提高学生的解题准确度,促进学生数学解题能力的提升。
二、数形结合思想概述
1.数形结合数学思想包含“以形助数”和“以数辅形”两个方面,其应用大致可以分为两种情形:一是借助形的生动性和直观性来阐明数之间的联系;二是借助于数的精确性和规范严密性来阐明形的某些属性。
2.数形结合思想是解答高考数学试题的一种常用方法与技巧,特别是在解选择题、填空题时发挥着奇特功效,这就要求我们在平时学习中加强这方面的训练,以提高解题能力和速度。具体操作时,应注意以下几点:
(1)准确画出函数图像,注意函数的定义域;
(2)用图像法讨论方程(特别是含参数的方程)的解的个数是一种行之有效的方法,值得注意的是首先要把方程两边的代数式看作是两个函数的表达式(有时可能先作适当调整,以便于作图),然后作出两个函数的图像,由图求解。
3.数形结合思想在高考试题中主要有以下常考考点:
(1)函数及其图像;
(2)解决方程的根或函数的零点问题;
(3)对于研究函数、方程或不等式(最值)的问题,可通过函数的图像求解(函数的零点、顶点是关键点),做好知识的迁移与综合运用。
(4)对于研究距离、角或面积的问题,直接从几何图形入手进行求解即可。
三、数形结合思想在数学解题中的应用
数形结合思想是一个重要的解题方法,可以锻炼学生的逻辑思维能力、分析问题的能力和作图能力。
在高中数学教学的过程中使用数形结合思想可以起到明显的作用。由于高中数学知识难度逐渐提高,教学内容越来越复杂,因此要注意有效融合相关的数学知识点,采用合理的方式解决数学问题。在高中数学知识中,包含了函数方程、几何等内容,教师要引导学生适时使用数形结合思想进行解题。在教学过程中使用数形结合思想,可以将难度逐渐降低,提高学生解题的速度和准确率。
四、案列分析
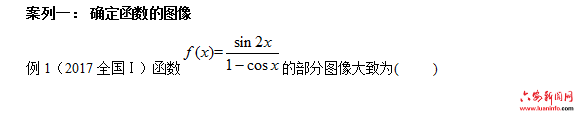




供有效的途径,还可以锻炼学生分析问题能力和动手作图能力。借助“形”的直观性来解决“数”的数量关系,借助“数”的精确性来解决“形”的位置关系,数形结合将代数问题和几何问题进行了有机统一。数无形时少直觉,形无数时难入微。数形结合百般好,隔离分家万事休。
(祝志好老师 编校)
