河西校区数学组 杨勇
前几天恰逢笔者所在学校两位老师举行公开课,所授课题为人教A版选修2-3中第二章第四节《正态分布》,从结果来看两位老师均基本完成本节课的任务,但从过程来看,教师不知道为什么教这节课,学生不知道为什么学习本节课,导致课堂氛围沉闷,教师抛出的问题犹如石沉大海,最后形成教师讲得激情澎湃,学生听得云里雾里的局面。课后,不少老师均反映本节课难教,其原因在于知识点的枯涩难以理解以及前后关联不强,总感觉本节在本章中的出现就像帽子里突然蹦出的兔子。教材主编章建跃博士曾经提出三个理解——理解数学、理解学生、理解教学,并且提出这三个理解的顺序不能颠倒,只有正确地理解数学,才能构建高效的课堂,否则只会是竹篮打水一场空。课后笔者又重新仔细地翻看教材,研读教参,下面从三个方面谈谈笔者对本节课的浅显认识。
一、“正态分布”的地位和作用
1.从学科特点的角度来看
概率的主要内容用数学角度分析生活中的随机现象,但是生活中的随机变量绝大多数都是连续的而并非离散的,如身高、体重、纤维的纤度、电容器的电容量……“正态分布”则正好是连续型随机变量的一种重要模型,正态分布的学习可以帮助学生客观地分析生活中的现象,做出正确的判断和决策。
2.从知识发展的角度来看
一方面,前面已经学习了离散型随机变量的分布列和期望方差,从知识的完整性而言,“正态分布”的学习有其必要性;另一方面,前面已经学习了二项分布,而正态分布与二项分布有着密不可分的关系,为高等数学中的中心极限定理提供基础。
3.从学生发展的角度来看
对正态分布定义及正态曲线的研究有利于培养学生观察、分析、抽象概括、推理论证、数形结合等数学能力,有利于培养学生严谨的数学态度和思维习惯。教学时应立足于引导学生自己提出要研究的问题、确定研究的方法、评价研究的成果、完善研究的过程,以促进学生发展的最大化。
二、关于引入
1.教材分析
教材中是以高尔顿板的实验作为引入的,这样的引入固然能引起学生的兴趣,为课堂增添活力,但是从本节课的内容特点来看,本节课所要学习的主要是连续型随机变量的分布情况,而高尔顿板的实验结果却是离散的——小球最终所落下的位置仅仅在有限个隔板之间,这难免会让学生纠结其是否为二项分布。后面教材中以球槽的编号为横坐标,做频率分布直方图来衬托“连续性”未免显得有些牵强。可能教材中的处理是从知识的本质出发,由概率论的知识可知,中心极限定理阐述了n重伯努利实验中,当n→+∞时二项分布会逼近于正态分布,通过高尔顿板的实验可以形象的解释二者之间的关系。但是从两位教师的课堂教学效果来看,并不理想,这样的引入并没有遵循数学知识的螺旋上升,课堂教学应立足于学生的最近发展区,所谓“跳一跳摘个桃”,以必修三统计章节中的总体密度曲线作为知识的立足点,教师合理的搭建支架,通过适当的问题引导学生探索发现,相信可以取到意想不到的效果。
2.引入设计
师:前面我们已经学习了离散型随机变量及其分布列,有哪些比较典型的分布列?
复习回顾,学生集体回答。
师:生活中有无非离散型随机变量即连续型随机变量的例子呢?
生:人的身高,体重、电灯的寿命、产品的尺寸……
师:以人的身高为例,某人的身高正好是175cm可能吗?为什么?
生:不可能,因为可能是175.000001cm(众生笑)
师:连续型随机变量的特征是在某区间内,取到任一点的概率均为0,所以我们更多的是研究其在某个子区间内的概率大小,那么如何研究呢?比如我们如何近似得到某人身高在[163,167](单位:cm)的概率呢?在前面的统计章节中有没有学习过相关知识呢?
若学生在这里遇到困难,教师可以适当引导。
通过已经统计的数据,利用计算机画出频率分布直方图,当样本容量逐渐增大时,将每个矩形上底的中点连起来可得到总体密度曲线。
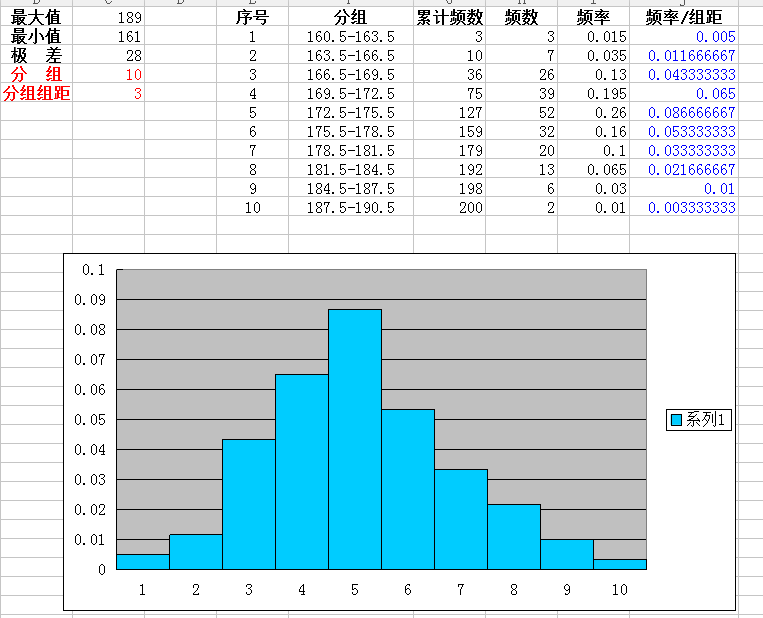
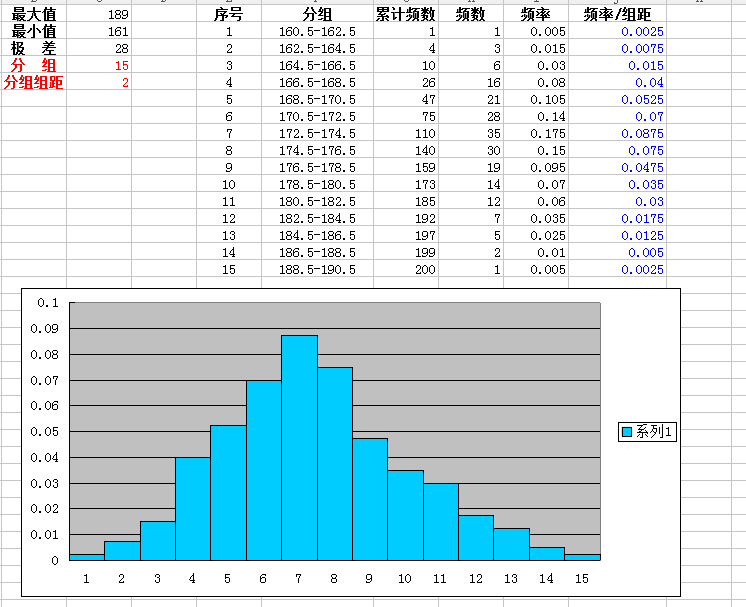
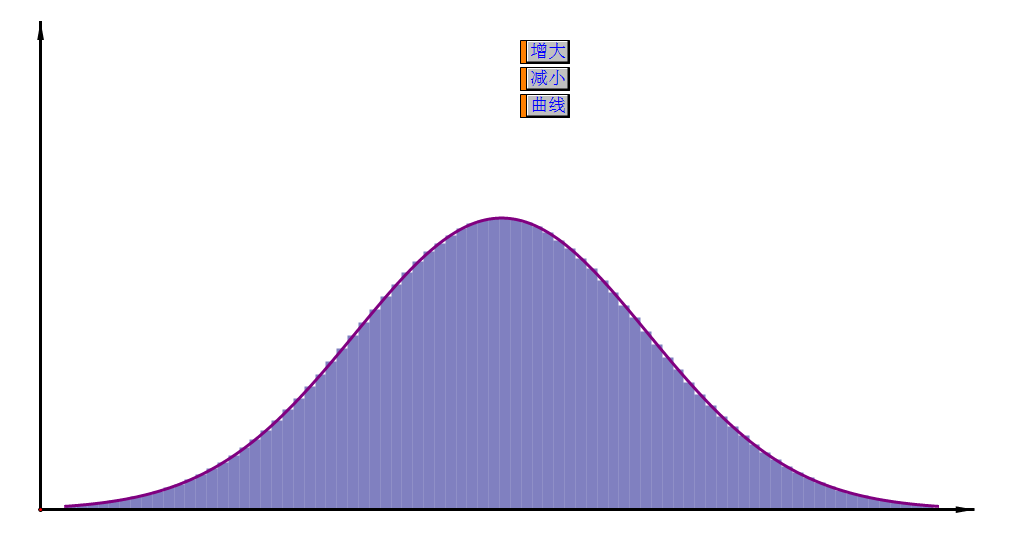
师:总体密度曲线有哪些特征?在某区间[a,b]内的概率可用什么来代替?
学生回答,教师指正。
师:当总体密度曲线对称,且是(或近似的是)下面函数的图像:
其中实数和(>0)为参数,我们称的图像为正态分布密度曲线,简称正态曲线。
三、关于定义
1.定义的得出
对于本节课的定义许多教师感觉不好处理,往往都是直接给出,有的甚至直接跳过,定义的教学核心是归纳概括,关键在于教师提出好的问题,引导学生观察总结,其实联系前面已经学习过的超几何分布和二项分布,不难发现其中的规律:
超几何分布:一般地,在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则则称随机变量X服从超几何分布。
二项分布:一般地,在n次独立重复试验中,用X表示事件A发生的次数,设每次事件A发生的概率为p,则p(x=k)=cknpk(1-p)n-k,k=0,1,2,……,n,则称随机变量X服从二项分布。
正态分布的定义形式与超几何分布、二项分布一样,均是利用概率的公式来定义,在某区间内的概率总体密度曲线中已经总结,只需要用符号化的公式进行表达即可,教师可以通过适当的引导,使学生观察归纳总结出定义水到渠成!
2.定义的挖掘
定义得出之后要提醒学生,一个随机变量如果是众多的、互不相干的、不分主次的偶然因素之和,它就服从或近似服从正态分布。然后教师一定要总结引例中为什么人的身高服从正态分布,因为身高受遗传、环境、饮食、锻炼时间等等各种不同的独立因素决定的,生活中服从正态分布的例子很多,可以让学生总结回答,让学生感受到正态分布广泛存在于自然现象、生产和生活实际之中,在概率和统计中占有重要的地位。
另外,定义的旁边一栏中提到了高斯在正态分布研究中的贡献,这是渗透数学文化的好机会,教师可以简单介绍高斯的生平:我国数学大师陈省身把黎曼和庞加莱称为数学家中的菩萨,而称自己为罗汉;高斯是黎曼的导师,有些教授把高斯称为数学家中的佛。在数学家中既能仰望理论数学的星空, 又能脚踏应用数学的实地的可不多见, 高斯是数学家中少有的顶“天”立“地”的人物,他既对纯理论数学有深刻的洞察力,又极其重视数学在实践中的应用。
高斯在数学上的贡献特别多, 去世前他要求给自己的墓碑上雕刻正十七边形, 以说明他在正十七边形尺规作图上的杰出工作。而后世的德国钞票上是以正态密度曲线来纪念高斯,这足以说明高斯的这项工作在当代科学发展中的分量。
四、关于正态曲线的性质
教材中给出了正态分布曲线的6个性质,其中前3个性质在教学的过程中应从形和数两方面入手,先让学生从正态分布曲线的图形中总结,然后再从函数的角度加以论证,教师不能顾此失彼,只是一味地从图像中观察而忽略从解析式的角度去分析性质。后2个性质主要是论证u和σ对图像的影响,教材中——包括许多教师的处理——是采用“控制变量法”,先让某个参数固定,变动另一个参数,利用计算机观察其对图像的影响,总体效果不错,但是笔者认为,如果在此基础上,从这两个参数本身的意义出发加以解释的话,效果会更好。事实上,u和σ分别是正态变量的均值和标准差,而均值又与正态曲线的对称轴有关,因此u的变化必然引起曲线对称输的变化,也就是使曲线的位置移动;f变大,说明数据的标准差变大,也就是集中程度减小。因此曲线肯定变得“矮胖”;f变小,说明数据的标准差变小,也就是集中程度增强。因此曲线肯定变得“高瘦”。不难看出,这一结论具有广泛性,把其应用到频率分布直方图判断近似均值和方差的大小也非常有效。
新课程强调的数学课堂是“自然的”,数学知识的呈现方式要自然,教学过程的设计要自然,不能局限于教教材,而是用教材教,教师只有充分地研读教材,理解教材,进而理解数学,才能设计出符合学生认知规律的“自然”课堂。
(祝志好老师 编审)
